Gauss-Hermite quadrature: an elegant parameterization for Gaussian integrals
Rich Pang
2026-01-22
Suppose we would like to numerically compute an intractable integral of the form
\[f = \text{E}_{\mathcal{N}(x)}[g(x)] = \int_{-\infty}^{\infty} \mathcal{N}(x) g(x) dx,\] where \(\mathcal{N}(x)\) is the standard normal distribution, and we would furthermore like to cleanly parameterize how accurately we will do so.
By using Gauss-Hermite (GH) quadrature, we can compute this integral using \(n\) function evaluations, \(g(x_1), \dots, g(x_n)\), such that higher \(n\) typically yields higher accuracy. Specifically, GH quadrature tells us that we should compute \[f \approx \sum_{i=1}^n w_i g(x_i)\] where \(x_i\) are the roots of the physicist's Hermite polynomial \(H_n(x)\) and the weights are given by \[w_i = \frac{2^{n-1}n!\sqrt{\pi}}{n^2 H_{n-1}(x_i)^2}.\]
Example
Here we evaluate the integral for \(g(x) = cos(x/2)(x/2)^2\). The plot below shows the roots of \(H_n\) for \(n=5\), and their associated weights.
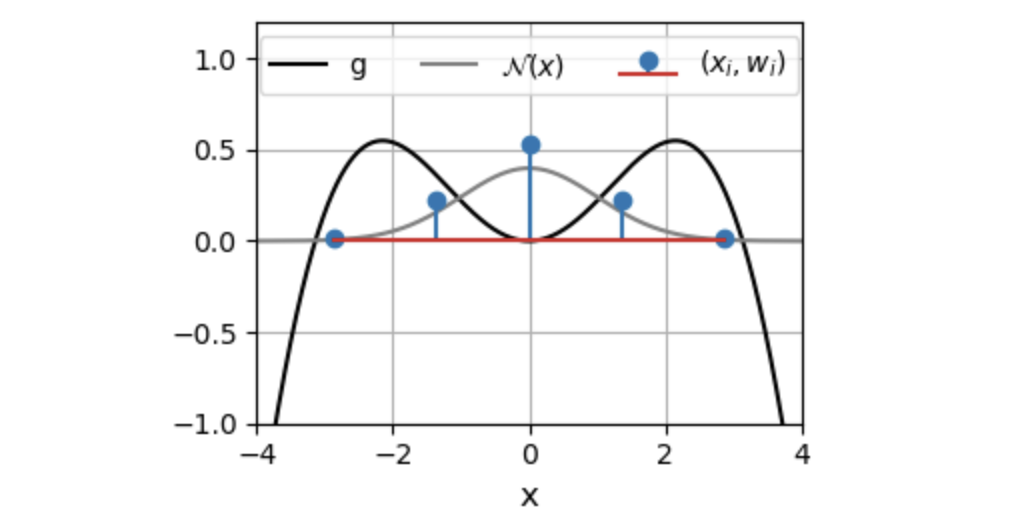
As we can see, the G-H approximation is quite accurate even for low \(n\).
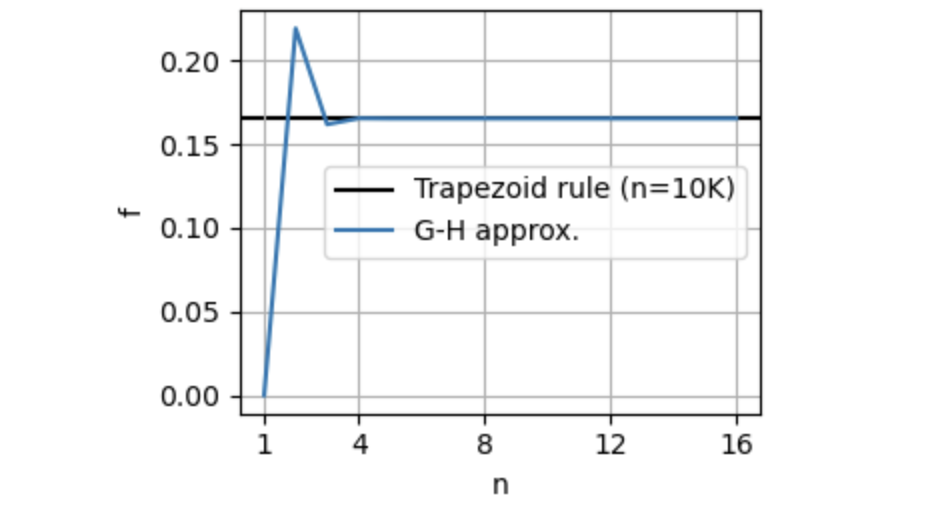
Comparison to other approaches
If we were to use the trapezoid rule, in addition to picking a resolution of our evaluation, we would have had to truncate the integration bounds, for instance from \(-L\) to \(L\), leaving us with another decision to make about how to choose \(L\). GH quadrature is thus simpler, since the accuracy of the approximation is controlled only by the single parameter \(n\).
Alternatively, we could have employed a Monte Carlo approach by sampling \(n\) values \(x_1 \dots x_n\) from \(N(x)\), then approximating \(f \approx \sum_i g(x_i)\). MC approaches, however, have the drawback of being nondeterministic — certain samples of \(\{x_i\}\) might yield better approximations than others. GH, on the other hand, is purely deterministic.
Python Code
The Python code for implementing GH quadrature is quite simple, since we can use numpy's hermgauss function:
import numpy as np
from numpy.polynomial.hermite import hermgauss
n = 16 # number of points
x_i, w_i = hermgauss(n)
def g(x):
return np.cos(x/2)*(x/2)**2
# evaluate (note the additional square-root factors needed)
f = (1. / np.sqrt(np.pi)) * np.sum(w_i * g(np.sqrt(2.0) * x_i))
Remark
GH quadrature is not necessarily optimal, and its accuracy will depend on \(g\). For instance, if \(g\) is a sum of \(n\) delta functions, the optimal function evaluations should take place at the locations of the delta functions. In practice, however, it is often quite accurate for well-behaved \(g\).